GUÍA EXAMEN GLOBAL
1. PRODUCTOS
NOTABLES. PUEDES PRACTICAR EN LA SIGUIENTE DIRECCIÓN http://www.educaplay.com/es/recursoseducativos/653862/productos_notables.htm
·
BINOMIO
AL CUADRADO. http://portalacademico.cch.unam.mx/alumno/aprende/matematicas3/productosnotables/page/0/1
·
DIFERENCIA
DE CUADRADOS.
http://portalacademico.cch.unam.mx/alumno/aprende/matematicas3/productosnotables/page/0/2
·
BINOMIO
CON TÉRMINO COMÚN.
2. SEMEJANZA Y CONGRUENCIA DE
TRIÁNGULOS. CRITERIOS DE CONGRUENCIA
Y CRITERIOS DE SEMEJANZA
3. TEOREMA DE PITÁGORAS.
APLICACIÓN. CATETOS, HIPOTENUSA.
APLICACIÓN DE LA HOMOTECIA. Las homotecias son un tipo
de transformación que preserva la forma, es decir, que los ángulos de las
figuras no cambian. Su característica principal es que tienen un centro y que
su razón está representada por el número k. ¿Qué sucede si k>1? La figura se hace mayor
1. USO DE
LA FÓRMULA GENERAL
·
Si el valor del discriminante es MAYOR que
cero, la ecuación tiene 2 soluciones
·
Si el valor del discriminante es MENOR que
cero, la ecuación no tiene soluciones
·
Si el valor del discriminante es IGUAL cero,
la ecuación tiene 1 solución
2. Teorema de Tales
“Si dos rectas cualesquieras se cortan por varias rectas paralelas, los
segmentos determinados en una de las rectas son proporcionales a los segmentos
correspondientes en la otra.”
3. Aplicaciones
de las razones trigonométricas :
·
Seno de
un ángulo: la razón entre el
cateto opuesto al ángulo y la hipotenusa.
·
El Coseno de un ángulo es razón entre el cateto adyacente o contiguo
al ángulo y la hipotenusa.
·
La Tangente de un ángulo es la razón entre el cateto opuesto y el Cateto adyacente o contiguo.
1.
Sucesiones de segundo
nivel o cuadráticas.
2.
Desarrollo plano de cilindros y conos.
Desarrollo
plano del cono.
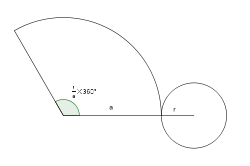
El desarrollo plano de un cono
recto es un sector circular y un círculo.
El sector circular está
delimitado por dos generatrices, siendo la medida del lado curvo igual a la
longitud de la circunferencia de la base.
La forma de calcular la distancia a en el desarrollo es con la ecuación de 
donde r es el radio de la base y h es la altura del cono.
El ángulo que está sombreado en
la figura se calcula con la siguiente fórmula:
1.
Volumen de cilindros y conos.
·
Cilindros V=Abh
·
Conos. V=(Abh)/3
2. Resolución de problemas que implican el uso de
ecuaciones lineales, cuadráticas o sistemas de ecuaciones.
Cuerpos de
revolución. Características de los cuerpos que se generan al girar sobre un
eje, un triángulo rectángulo, un semicírculo y un rectángulo
.
No hay comentarios:
Publicar un comentario