OBTENCIÓN DE LA REGLA GENERAL DE UNA SUCESIÓN CON PROGRESIÓN ARITMÉTICA.

PRIMER GRADO BLOQUE V

Tema 4 Obtención de la regla general (en lenguaje algebraico) de una sucesión con progresión aritmética.

 Identifiquen el comportamiento de los términos en una sucesión de figuras y encuentren términos faltantes.

 

Actividad: En equipos, analizar las siguientes sucesiones y dibujar los términos que faltan. Explicar y justificar los procedimientos empleados

Consideraciones: Una progresión aritmética es una sucesión en que cada término (menos el primero) se obtiene sumando al anterior una cantidad fija d, llamada diferencia de la progresión.

• Si d>0 los números cada vez son mayores, se dice que la progresión es creciente.

• Si d<0 cada="" decreciente="" dice="" es="" la="" los="" menores="" meros="" n="" o:p="" progresi="" que="" se="" son="" vez="">

2, 4, 6, 8, … → d=2

d>0 CRECIENTE

7, 5, 3, 1, … → d=-2

d<0 decreciente="" o:p="">

Identifiquen y expresen en lenguaje común la regla general de sucesiones con progresión aritmética.

Actividad1: El siguiente esquema representa lo que realiza una máquina al introducir las posiciones de los primeros cinco términos de una sucesión. En equipo, encontrar los números de la sucesión que corresponden a las posiciones 50, 100, 500 y 1000, respectivamente

Actividad 2: De acuerdo con el siguiente esquema, escribir la regla general que permite determinar cualquier número de la sucesión, en función de su posición.

Taréa:

Escribe el término general de las siguientes progresiones aritméticas:

a)    4,6,8,10,.... ____________________________________

b)    3, 1, 5, 9,.... ___________________________________

c)    5,8,11,14,.... __________________________________

Expresen en lenguaje algebraico, la regla general de sucesiones con progresión aritmética.

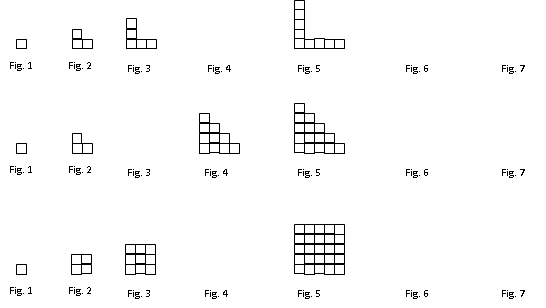
Actividad 1: Organizados en equipos, escriban con una expresión algebraica la regla general que permite determinar el número de cuadritos de cualquier figura, en función de su posición, de la siguiente sucesión:

Actividad 2:

Escriban algebraicamente la regla general que permite determinar cualquier término de cada una de las siguientes sucesiones:

a)    2, 4, 6, 8, 10

Regla: _______________________

b)    5, 10, 15, 20, 25

Regla: _______________________

c)    3, 5, 7, 9, 11

Regla: _______________________

d)    6, 11, 16, 21, 26

Regla: _______________________

Observaciones posteriores:

El término general de una progresión aritmética es: an = a1 + (n-1)·d

donde a1 es el primer término y d la diferencia.

Ejemplo: 4,8,12,14      an=4+(n-1)4     an= 4+4n-4    an=4n